■等積変形■
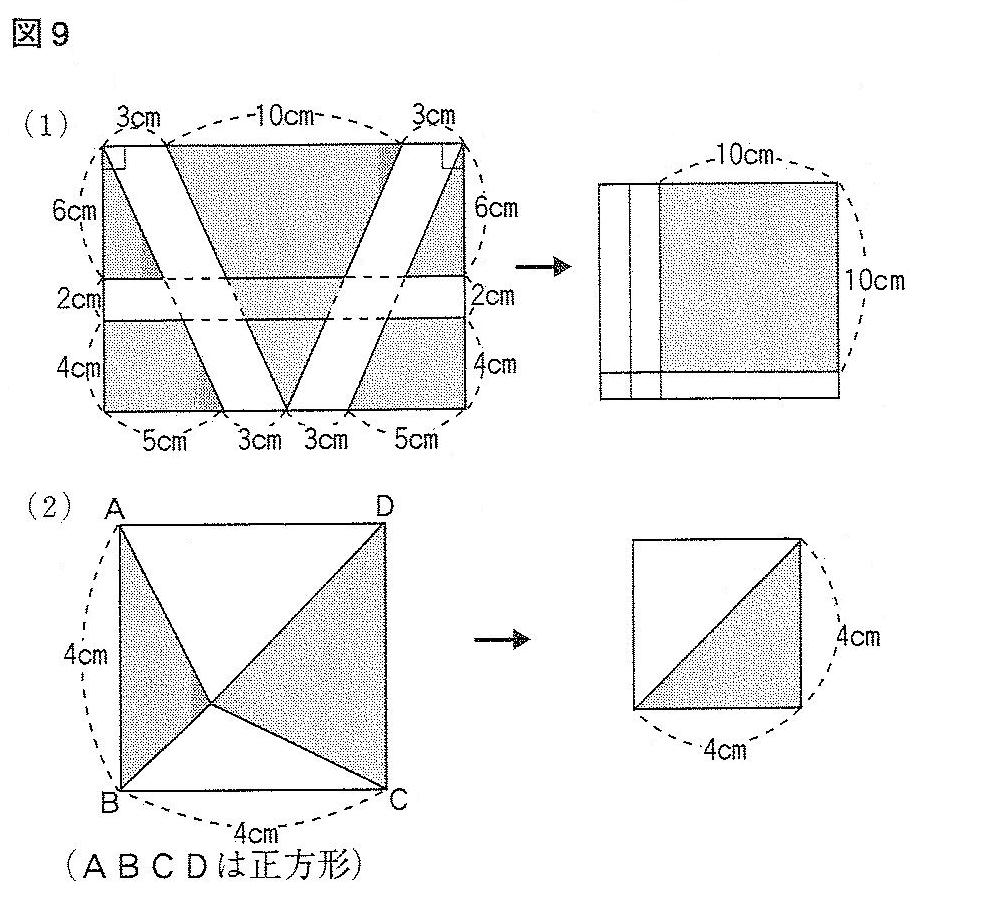
図9のような問題では、形は違っても面積は同じであるということに着目させます。これを「等積変形」といいます。平行線の間においた三角形で説明することが多いですね。この技は高校入試まで利用していきますから、きちんとした理解、そして訓練が必要です。(1)では、必要のない部分を図の端に寄せて考えます。私の授業では「テトリス」という話をしますが。。。最近「そんなゲーム、知らない」と言う生徒が増えてしまい、歳を感じてしまう。。。平行四辺形の面積は「底辺×高さ」です。この問題の場合は長方形と考えて「たて×よこ」としても面積は変わらないわけです。(2)の様な問題では、平行線の性質を利用します。この「平行線の性質」は中2でも学習する内容です。高校入試にも頻出、ということです。三角形の形は変わっても、平行線の幅は一定だから、高さは変わらないという性質が、利用価値の高いものとなっているわけです。私の授業では「問題に平行線が書かれていたらアヤシイと思え」と構えさせます。見事に変形し切れたとき子供達から「おおぉ」という感動の声を聞くことが出来ます。
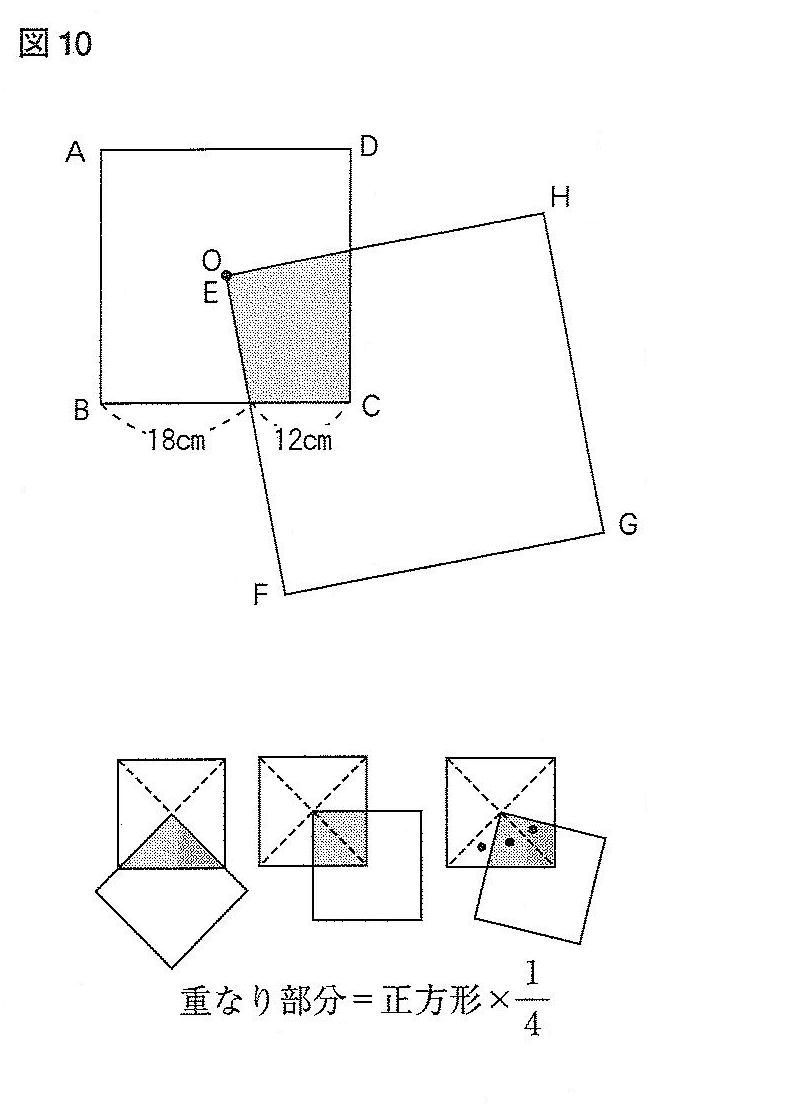
また図10のように、正方形を組み合わせた問題では、中心を通っている限り、どんな位置にあっても面積は4分の1になることを利用しています。図の例では、18cmと12cmに分けていますが、関係ありません。この問題、20年近く前に「ラ・サール高」で使われた問題です。私の授業では、少しずつ形を変えた図を追いかけていきます。説明では「リンクしている」といいます。こっちが小さくなったら、こっちが大きくなっている、というような説明です。文字ではなく、図で、実際の形を使って感覚を養っていくわけです。
■いわゆる30度問題■
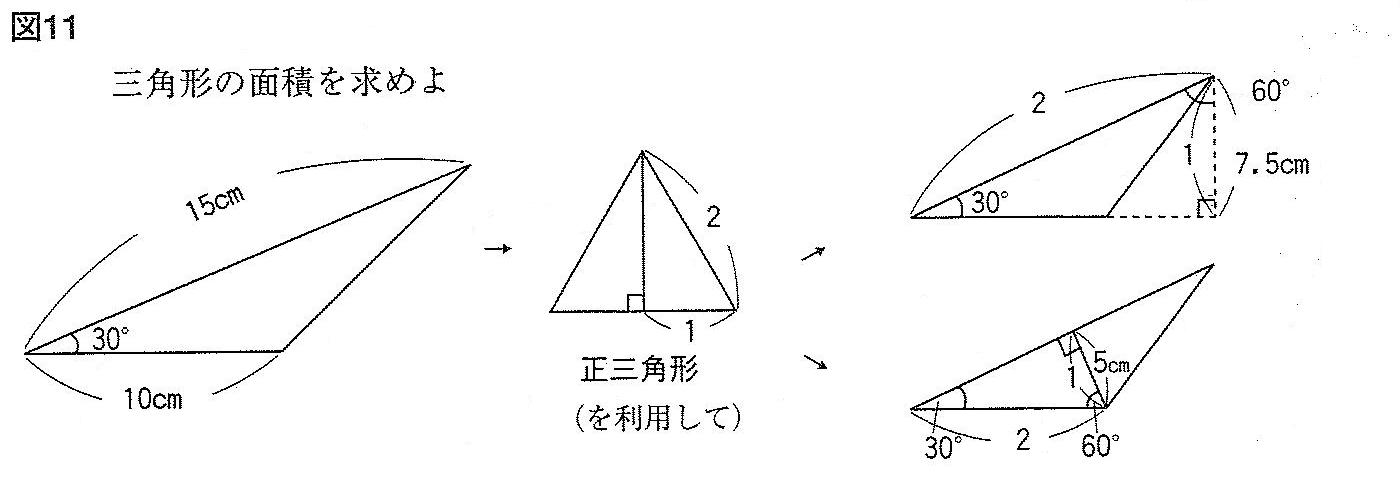
たとえば図11のように、1つの角度を30度と、2辺の比が2:1の関係になっている三角形では、例え高さが書かれていなくても、正三角形の半分(三角定規と同じ)・直角二等辺三角形を利用すれば解決できます。実は高校入試において、この定規の利用は非常に多く、暗記事項として扱われるものです。この他、3:4:5の直角三角形、5:12:13の直角三角形の辺の比率も使われます。小学生に平方根は使えませんから、片手落ちになってしまいますが、これが「三角比」の出発点であることは間違いありません。覚えて使いこなすという点においては、「九九」「乗法公式」などと同じ。まさに、日本の数学を解いていると感じる問題です。
■立体の切断■
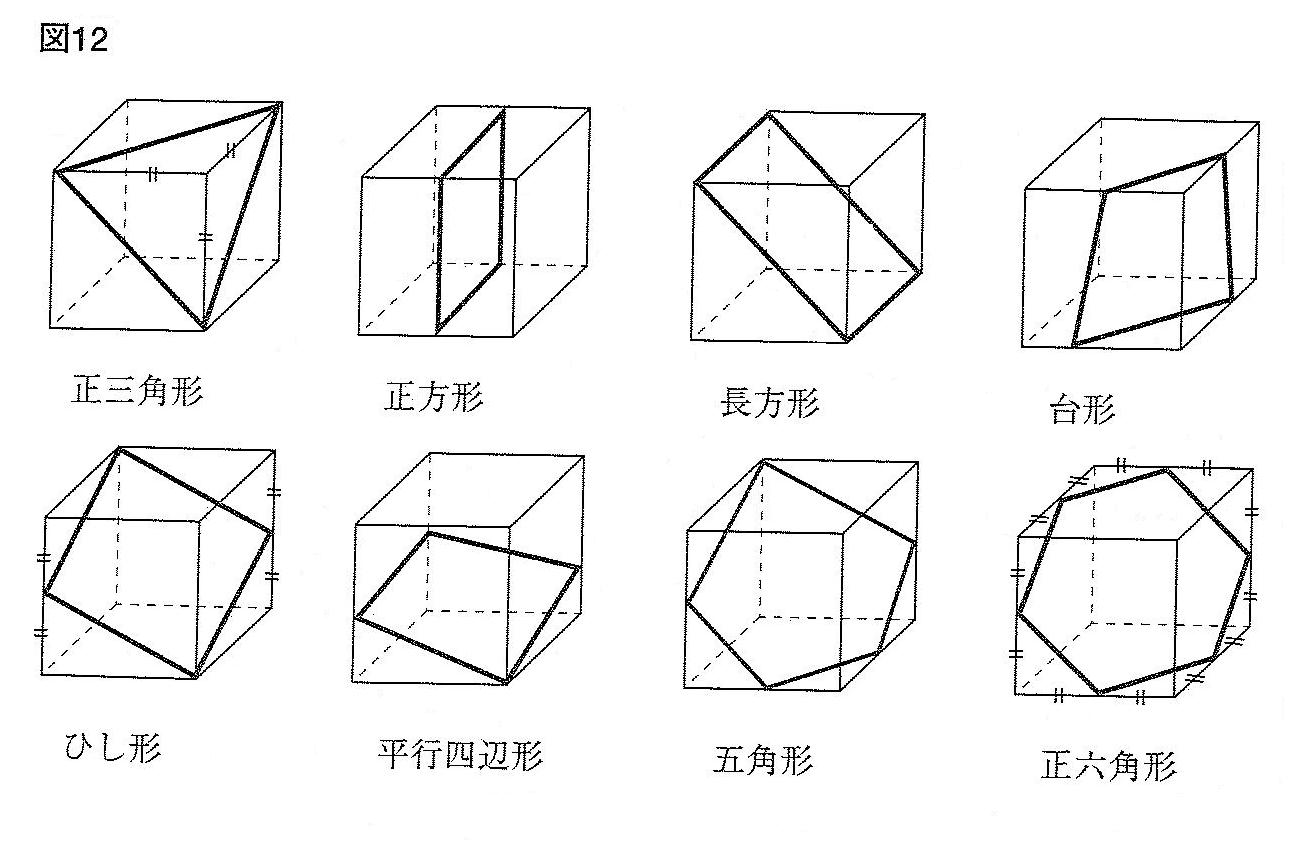
立体を切断した切り口の問題は、最近は減ったようです。それでも必須パターンであることは間違いありません。色々ありますが、図12のものを基本として覚えるべきです。かつては中1で「空間図形」として訓練された内容ですが、ここのところ手薄になっています。また、帰国枠中学入試では「立体は扱わない」という学校もあります。
私のクラスでは、5年生の夏休みの課題として出題することがあります。「お母さんに頼んで、ジャガイモのサイコロを作ってもらえ」と出題します。これをプラスチックナイフなどで切断してみるわけです。なぜ直角三角形が出来ないのか。なぜ7角形以上は出来ないのか。微妙に難しい平行四辺形。スーパーマンマークとは?などなど、実験してきて貰うのです。この体験が、小6夏期講習(受験クラス)での演習問題に生きます。
立方体の見取り図も練習が必要です。慣れないと、歪んだサイコロになります。どの辺とどの辺が平行なのか、長さの等しい辺は何処なのかなどの確認をしておきましょう。
切断面の面積を求める場合、立体のまま考えるのではなく、平面にします。この手順が後に立体は平面お集まり、つまり「積分」へと繋がっていくわけです。中3の受験問題でも私のクラスでは「人は、立体を立体として使えていない」などと説明し、空間の対角線にしても、切り口にしても、平面にしてから求めていることを説明します。
その他、円柱を斜めに切った問題もよく見かけます。(私のクラスでは『かぐや姫』といっています)これは有名な解法。同じ立体を重ね合わせて求めやすい形にし、最後2で割って解答にたどり着くというものです。
立体の問題は、問題を「消化」することが一番。まず『理解すること』が肝心なんですね。そして「慣れ」です。これは「量」ということですね。基本問題程度であれば、2,3問で慣れてしまうこともありますが、入試レベルであればあり得ません。いくつもいくつも「やりこなすこと」が必要です。そして最後に「イメージトレーニング」です。これについては、後述します。
■相似■
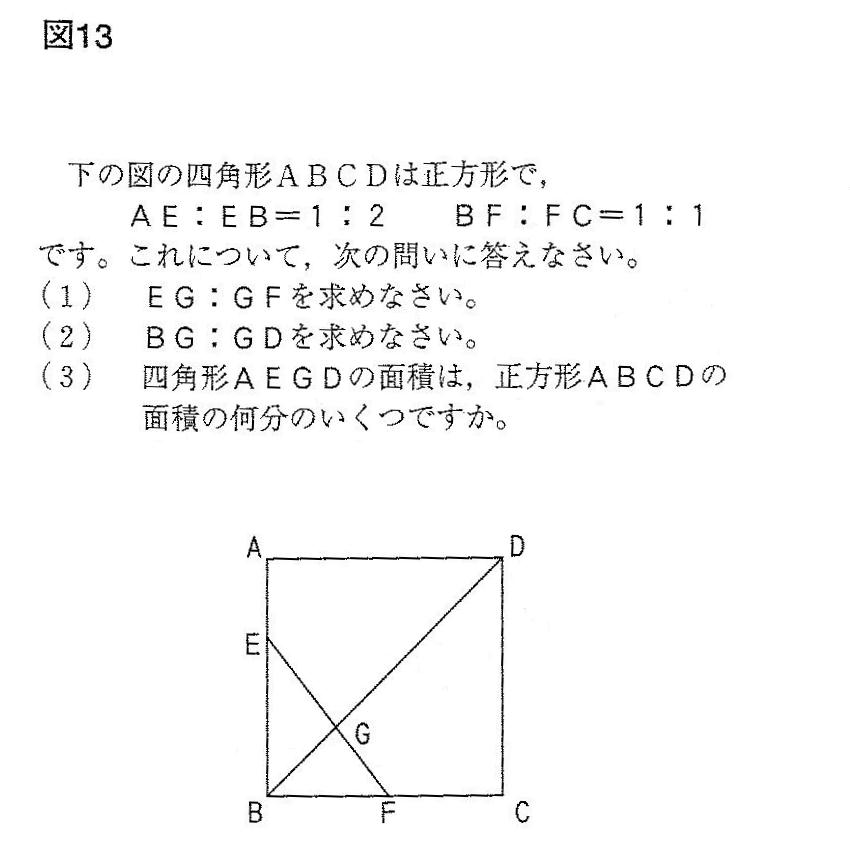
図13のような問題は、中学入試でも高校入試でも頻出です。単純な三角形のみのものだけではなく、正方形や長方形、平行四辺形の中に直線が交差している問題では、相似な三角形を見つけて、その相似比を利用することがポイントになります。ただし多くの問題では「補助線」を引いたりしますので、訓練が必要です。何処に補助線を引くのか、例題や授業で解説した問題を使って、納得するまでやり直します。同じ問題でも解決方法を2つ3つ作ることが出来るのか。三角形に分割できても、左右反転してわかりにくくなっているものもあります。色々な角度から図形を見ることが大切です。私のクラスでは「ノートを逆さまにしろ」「テキストを右90度回転させろ」となどいうこともあります。
以上は押さえておきたいポイントのほんの一部です。どれも基本的なものばかりですが、難しいとされる融合問題でも、これらの基本パターンの『組み合わせ』でしかありません。授業ノート・テキスト・プリント、そして持っている問題集など、様々な問題をこなし「身に付くまで繰り返し練習」するしか対策はないわけです。
■必ず自分で図形を描くこと■
図形が描かれていない図形問題。文章だけの図形問題というものがあります。それならば、いうまでもなく図を書いて考えるべきです。はじめから図形がシメされている問題でも、必ずノートに図形を書き写して考える習慣を付けるべきです。テキストや問題用紙の図形を塗りつぶして汚すことは、イメージする力を固定してしまい、着眼・発送などが伸びていきません。
このときのポイントは「フリーハンドで描く」ことです。普段からフリーハンドになれておけば、短時間で正確な図が描けるようになってきます。定規などの道具を使わない第一の理由は、「時間がかかる」からです。これは入試では致命傷です。第二の理由は、「手が感覚を覚えないから」です。等距離にあるか、それとも遠くにあるのか、問題図は「うそ図」であることが当然。そこで描き直していくときに、「このくらい」という感覚があれば、次のステップに繋がりやすいのです。
普通のノートの罫線を上手に利用しましょう。罫線とは平行線です。平行線を利用して見取り図を描くと綺麗に描けます。
図形問題では、補助線や、どの三角形を使うのかなど、様々な面を考えていきます。前述の通り、1つの図に色々書き込むのは止めましょう。設問ごとにササっと図を書き直す癖を付けましょう。色を使い分けるのも効果的。筆箱には常に3色以上のペンなどを用意しておくと便利でしょう。
■分からない問題は必ず質問■
いくらパターン学習を積んで基本知識を身につけていても、ちょっとした問題を解くヒント、切り口、突破口を見つけられなければ、入試問題は解けません。
どうやれば解けるのかをあれこれ考えることは非情に大切なことです。そして算数を得意科目にする姿勢でもあります。もしあなたが5年生よりも下の学年であれば、是非、じっくり時間をかけて考える習慣をつけてください。5年生以上になったら、時間的な余裕がありません。ある程度の時間を区切りましょう。1問に20分もかけることは良いことではありません。試験のことを考えても10分が限界でしょう。考えて、分からなければ質問してください。enaでは、自習室・図書室があります。また、殆どの時間、3人の先生のうち1人は、職員室に常駐しています。塾は利用するもの。そこで理解して、理解できたらすぐに、もう一度やり直してみる。確かめる。こういう習慣を身につけて欲しい。質問しにきても、答えだけ聞いて「ああ、わかりました」と放置してしまうようなやり方は、伸びる方法ではありません。止めましょう。
■ヒントを与えながら■
3年生ぐらいだと、まだまだ一人で勉強するには厳しい年齢。やはり隣に大人がついて勉強する方が効率が良いようです。
ただし注意すべきことは、大人が勉強を見るとき、いきなり答えを教えるのではなく、少しずつヒントを与えながら、子供自身が答えに到達できるように配慮してあげることです。このさじ加減は、実はとても難しい。勘定が先走り、「だからね!」と全てを教えてしまうと、子供自身で解法に気が付くことが出来ず、いつまで経っても苦手意識を残してしまうのです。
■友達と一緒に勉強する■
5年生で「自学・自習が完成していること」というのが、私たちの考える理想論です。ところが5年生以降、子供達にとっては難しい問題が多く、それだけ行き詰まりやすくなります。そこでお勧めするのが友達同士の勉強です。もちろん遊んでしまわないように注意する必要があります。
教えあうこと、一緒に考えることは意外と効果が高いようです。お互いに刺激になります。それ以上に、一人で頭の中だけで考えているのではなく、口に出して情報を整理することが、解法の糸口を見つけやすくしているメリットがあります。本当に理解しているかどうかは、子供に説明させることで判断が付きます。きちんとりかいできていれば、順序立てて上手に説明できます。このことは学年を問わず、言えることです。また二次的効果として、国語の勉強にも繋がります。作文は、まさにアウトプット。インプットの知識の詰め込みに対して、表現を訓練するところ。数学の証明も同じ。これらは「自分には分かるけど」という独りよがりではなく、客観的に分かるかという視点に立つことが必要です。
■日常生活を通して■
前述のジャガイモ宿題だけではなく、車のワイパーから線分の通った図形を想像させたり、家の見取り図や展開図を描かせてみたり。。。図形問題攻略のカギは、家の中にごろごろ転がっています。大切なのは、周りの大人がそれらを意識して子供たちに接することです。ある中学の先生がおっしゃいました。「見えない部分を想像することができるか」つまり、見取り図の「点線」を意識できているか、ということです。日頃から点線で描いていると何でもないことですが、見えないものは書けない!と開き直っている生徒は必ず壁に当たってしまうわけです。
頭の中でイメージすること。このトレーニングが何よりも大切です。最近のビデオゲームは3Dが普通。立体把握しやすい環境になっているはずです。それをさらに意識させることができるかは、周りの大人こそが意識しているかどうか、ということではないでしょうか。つまり子供たちにイメージトレーニングの機会を数多く設けていくことが大切だというわけです。結局、攻略法の最後は、これにつきるわけです。
<TOPへもどる>